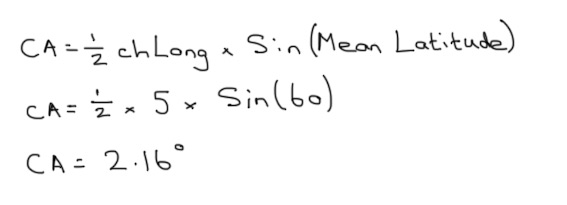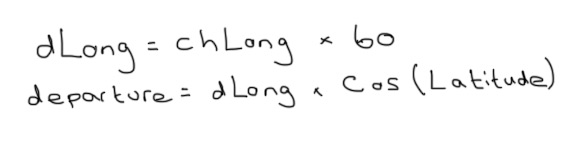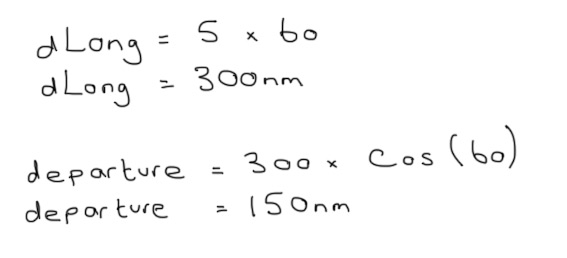Waypoint 1: 60°S 030°W

Waypoint 2: 60°S 020°W

What will be the approximate latitude shown on the display unit of an inertial navigation system at longitude 025°W?

Let’s start with a really quick primer for anyone not already up to speed with General Navigation. Because the Earth is roughly spherical (geeky fact – it’s an Oblate Spheroid), the shortest distance between two points on its surface isn’t a straight line. If you were to stretch a piece of string between two points on a ball, you’d end up with the string describing part of a circle who’s centre would match the centre of the ball itself. This is called a Great Circle, and this is the same route an aircraft takes between two points on the Earth. Maths for the ATPL course is simplified to a practical level – there’s no spherical Trigonometry, but the syllabus still teaches the key concepts in long range navigation.

We’ll draw a picture of the information in the question, as this will help us to visualise it better…

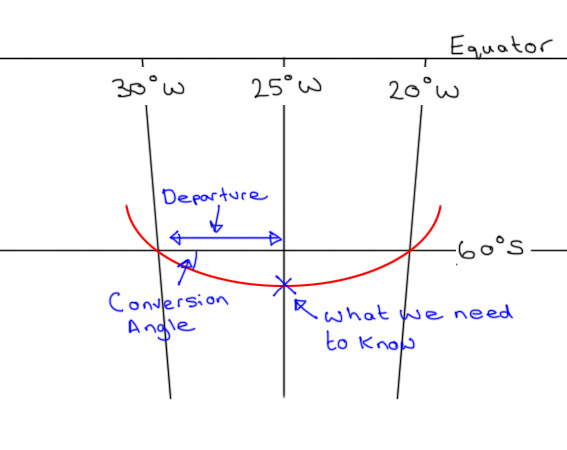
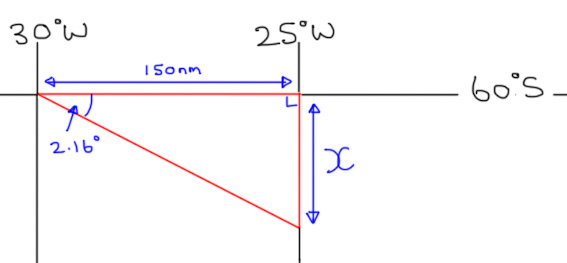
I’ve drawn the Great Circle track between the two waypoints on in red. When you draw a Great Circle, it always bends away from the Equator. We’re in the Southern hemisphere, so we can instantly see that at 025°W the aircraft will be further South than 60°. The ATPL syllabus equips us to find the two unknowns we need to solve this problem…

If we can find the Conversion Angle and the Departure shown on the diagram above, we can use basic Trigonometry to find out how far South of 60° the point on the Great Circle track actually is. Let’s start with the Conversion Angle, which is the difference between the Great Circle Track and the associated Rhumb Line. I don’t want to complicate things too much, but a Rhumb line between two points crosses every Meridian at the same angle. Therefore, a Parallel of Latitude is a Rhumb Line. In the case of our question, the change of Longitude, or chLong is from 030°W to 025°W, or five degrees. Both points under consideration are at 60°S, so the mean Latitude is 60.

Next, we can work out the distance along the Parallel of Latitude between 030°W and 025°W. At the equator, each degree of Longitude is 60 Nautical Miles (so around the Equator is 60 x 360 = 21,600nm). Firstly we work out what five degrees of Longitude would be at the Equator. But the Earth is a sphere, so as you head away from the Equator, each Parallel of Latitude has a smaller circumference. The Departure formula allows us to use Trigonometry to work this out, but is only valid for points of the same Latitude. The syllabus doesn’t go deeper than this so questions of this type will always involve two points at the same Latitude…

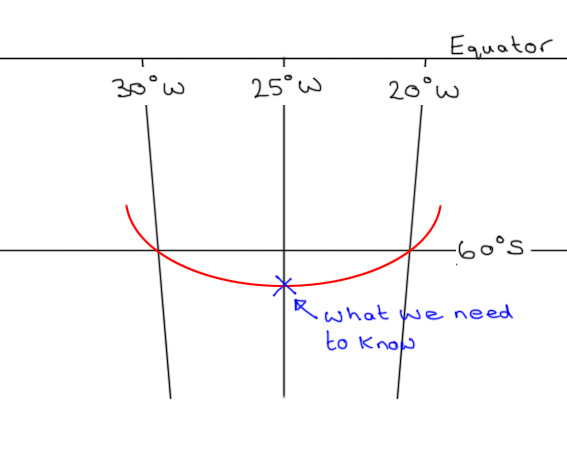
Let’s fill in the information we’ve worked out so far…

We don’t have the tools to work the answer out perfectly, which is why the question asks for an approximate answer. If we can find X, we can find out how many Nautical miles South of 60° the aeroplane will pass. Using GCSE Trigonometry (I still use SohCahToa to work out which function I need)…

So the point we’re looking for is 5.65nm South of 60°S. Because Meridians of Longitude don’t vary the way that Parallels of Latitude to, we can assume that 60nm is equal to one degree of Latitude. So 5.65nm is approximately 5.65 minutes of Latitude, where one minute is 1/60th of a degree. So our final answer is…

60°05.65’S, or 60°06’S to the nearest minute.

I think this is a pretty good question, as it tests lots of different parts of the GNav syllabus, and ensures you can put all of the different parts together. It’s fairly long winded though, so I hope it’s worth a few marks!