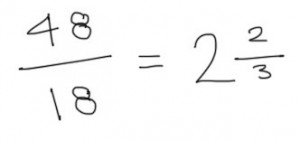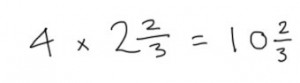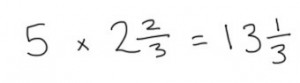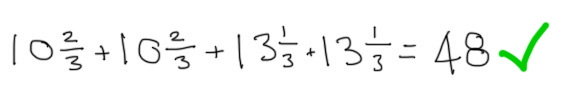I recently received an email from a friend of mine who was trying to solve a maths problem he’d encountered preparing for pilot aptitude testing. The problem was along the lines of this…

“A rectangle has a ratio of 5:4. If the perimeter of the rectangle is 48cm, what is the length of the shortest side?”

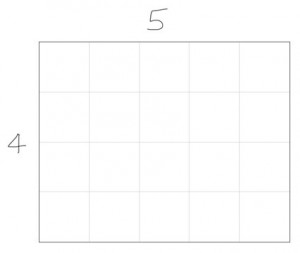
Let’s break this down a bit. Start by imagining a simple rectangle with the ratio 5:4. Please excuse my drawing…

By adding up the length of the sides, we can see that the perimeter of this rectangle is 18cm. But the rectangle in the question has a perimeter of 48cm. If we divide 48 by 18, we can work out how much bigger the 48cm perimeter rectangle is than the 18cm one…

If the 48cm perimeter rectangle is 2⅔ bigger than the 18cm one, each side must be 2⅔ bigger too. The shortest side of our 18cm perimeter rectangle is 4cm, so multiplying this by 2⅔ gives us our answer…

We can work out the length of the longer side by performing the same calculation, this time multiplying 5cm by 2⅔…

Finally, we can check our working by adding the values of our calculations together to check that the perimeter of the resulting rectangle is 48cm…

Lots of problems involve ratios. The important thing to remember in this case is that as the perimeter of a rectangle increases, each of its sides will increase by the same factor.